Algo de combinatoria y números primos

Introducción

Los métodos tipo criba hacen parte de las primeras técnicas matemáticas empleadas en el estudio de la distribución de los números primos. Estos métodos buscan encontrar una estructura al conjunto de los estos números estudiando su comportamiento hasta un determinado entero.

En el siguiente documento, un trabajo en colaboración con mi estudiante tesista Cristian Andrés Valor, hacemos un recorrido de las ideas desarrolladas por el matemático Ernst Meissel para obtener una expresión que nos permita reescribir la criba de Eratóstenes (véase ecuación 14)

Residuos en progresiones aritméticas

Para un par de números enteros $p$ y $q$ con $p > 0,$ denotaremos con $\left[ q , p \right]$ al residuo de la división de $q$ por $p.$ Identificaremos con $\varphi(n)$ para $n \geq 1,$ a la función idicatriz de Euler, que corresponde el número de enteros positivos menores o iguales que $n.$ Es claro que si $p$ es primo entonces $\varphi(p) = p-1.$ Por otro lado, es bien conocido que $\varphi$ es multiplicativa en el sentido de que si $(m,n) = 1$ entonces $\varphi(m n) = \varphi(m) \varphi(n).$

Identificaremos con $\pi(x)$ al número de primos menores o iguales que un cierto número $x,$ y con $\pi(x ; q, r)$ al número de primos menores o iguales que $x,$ presentes en la progresión aritmética $\{ qk + r\}$ con $(q,r)=1.$

Denotaremos con $P{\left(x\right)}$ al conjunto de primos menores o iguales que un cierto número $x,$ y con $P^*(x)$ al conjunto de primos no pares menores o iguales que $x.$ Es claro que $\big \vert P \left( x \right) \big \vert = \pi \left( x \right)$ y que $\big \vert P^* \left( x \right) \big \vert = \pi \left( x \right) -1.$

Denotaremos con $x\#$ al factorial primo de $x,$ esto es \[ x\# = \prod_{p \in P(x)}p, \] Note que \[ \varphi(x\#) = \prod_{p \in P(x)}(p-1). \]

Para un par de enteros $q$ y $x,$ escribiremos $d_q(x)$ para representar la función \[ d_q(x) = \begin{cases} 1 \text{ si } q \vert x, \\ 0 \text{ en caso contrario}. \end{cases} \] Para un entero $q$ menor o igual que $x,$ identificaremos con $C(x ; q, r)$ al conjunto de los números, menores o iguales que $x,$ presentes en la progresión $\{q k + r\}$ con $k = 0, 1, 2, \ldots.$

Escribiremos $\beta(x)$ para referirnos a la función \[ \beta(x) = \begin{cases} 0 \text{ si } x \text{ es primo}, \\ 1 \text{ en otro caso,} \end{cases} \] y escribiremos $C^*{\left(x; q, r \right)}$ para identificar al conjunto \[ C^*{\left(x; q, r \right)} = \begin{cases} C{\left(x; q, r \right)} \setminus \{ r \} \text{ si } \beta{\left( r \right)} = 0, \\ C{\left(x; q, r \right)} \text{ si } \beta{\left( r \right)} = 1, \end{cases} \] Note que \[ \big \vert C^*{\left(x; q , r \right)} \big \vert = \left \lfloor{\frac{x - r}{q}}\right \rfloor + \beta{(r)}. \tag{1}\] Emplearemos la notación $D \left(x; q \right)$ para representar el conjunto de divisores primos de $q$ menores o iguales que $x,$ es decir $D{ \left( x; q \right) } = \left\{ p \in P{ \left( x \right)} : p \vert q \right\}.$

Para un entero $j$ no negativo, representaremos con $A_j(x ; q)$ a los conjuntos \[ A_j(x ; q) = \begin{cases} \{1\} \text{ si } j = 0, \\ \\ \left\{ \prod_{i = 1}^{j}p_i : p_i \in P {\left( x \right)} \setminus D(x;q) \right\} \text{ si } j \geq 1. \end{cases} \]

Identificaremos con la letra $Q$ a los elementos de $A_j(x;q)$. Note en particular que si $j = 1$ entonces $Q$ es un número primo perteneciente al conjunto $P(x) \setminus D(x;q).$

Lema 1 Sean $q,$ $r$ y $x$ enteros no negativos tales que $r < q \leq x.$ El número de primos presentes hasta $x,$ en la progresión $\{ qk + r\}$ con $(q,r) = 1$ es \[ \pi(x ; q , r) =1 - \left \lfloor{\frac{1}{r}}\right \rfloor + \left \lfloor{\frac{x - r}{q}}\right \rfloor + \sum_{j = 1}^{\pi{ \left( \sqrt{x} \right)} - d} (-1)^j \sum_{Q \in A_j(\sqrt{x} ; q)} \Big\vert C^*{\left(x ; qQ , \left[ rQ^{\varphi(q)} , qQ \right] \right)} \Big\vert \tag{2}\] en donde $d = \big \vert D{\left( \sqrt{x} ; q \right)} \big \vert .$

Prueba. Si para un cierto entero no negativo $z$ el número $1 < pz + r \leq x$ es compuesto, entonces existe un primo $Q \in A_1(\sqrt{x} ; q)$ que le divide, y es claro que $pz + r$ es una solución del sistema de ecuaciones modulares, \[ \begin{cases} x \equiv r \ (\mathrm{mod}\ q), \\ x \equiv 0 \ (\mathrm{mod}\ Q). \end{cases} \tag{3}\] De acuerdo con el Teorema chino del residuo este sistema admite solución siendo una de estás $rQ^{\varphi(q)},$ con lo que un conjunto de soluciones no negativas de 3 hasta un cierto $x,$ esta dado por $C{\left(x ; Q , \left[ r Q^{\varphi(q)} , qQ \right] \right)}.$ Se sigue entonces que el conjunto de números primos, hasta un cierto $x$ presentes en la progresión $\{qk + r\}$ corresponde con \[ \pi{\left(x ; q, r \right)} = \Big\vert C(x ; q, r) \setminus \bigcup_{Q \in A_{1} (\sqrt{x} ; q)} C^*{ \left( x;Q, \left[ r Q^{\varphi(q)} , qQ \right] \right)}\Big\vert - \left \lfloor{\frac{1}{r}}\right \rfloor \tag{4}\] En donde se ha restado término $\left \lfloor{1/r}\right \rfloor$ contemplando la posibilidad de que $r = 1.$ También se ha empleado la notación $C^*$ pues es posible que $ rQ^{(q)} = $ sea un número primo, el cual no debe ser excluido del conjunto $C(x ; q, r).$

De acuerdo con el principio de inclusión–exclusión, podemos reescribir el cardinal en 4 sumando y restando de forma alternada, al cardinal de $C(x;q,r),$ el cardinal de las intersecciones dos a dos, tres a tres y de esta forma sucesivamente hasta las $\pi(\sqrt{x}) - d$ con $d = \vert D(\sqrt{x} ; q)\vert$ intersecciones de los conjuntos $C{\left( x;Q, \left[ r Q^{\varphi(q)} , qQ \right] \right)}.$ De acuerdo con este propósito, note que para $Q_i \in A_1{\left( \sqrt{x} , q \right)}$ con $i = 1, \ldots n,$ se tiene como una consecuencia directa del Teorema chino del residuo, que el sistema de ecuaciones modulares \[ \begin{cases} x \equiv & \left[ rQ_1^{\varphi(q)} , qQ_1 \right] \ (\mathrm{mod}\ Q_1), \\ & \vdots \\ x \equiv & \left[ rQ_n^{\varphi(q)} , qQ_n \right] \ (\mathrm{mod}\ Q_n), \end{cases} \tag{5}\] admite solución, siendo una de estás $rQ^{\varphi(q)}$ con $Q = \prod_{i = 1}^{n} Q_i$. Note que en este caso $\left[ rQ^{\varphi{(q)} } , pQ \right]$ será un número compuesto. Esto sugiere que el conjunto de soluciones no negativas de 5 hasta un cierto $x$ corresponde con $C{\left(x ; Q , \left[ r Q^{\varphi(q)} , qQ \right] \right)}$ para $Q = \prod_{i = 1}^{n} Q_i,$ y en este caso , se sigue de 1 que \[ \Big\vert C^*{\left(x; qQ , \left[ Q^{\varphi(q)} , qQ \right] \right) }\Big\vert = \left \lfloor{\frac{x - \left[ Q^{\varphi(q)} , qQ \right] }{qQ}}\right \rfloor + 1. \]

Por lo tanto, si $x < \left[ Q^{\varphi(q)} , qQ \right]$ entonces $\Big\vert C^*{\left(x; qQ , \left[ Q^{\varphi(q)} , qQ \right] \right) }\Big\vert = 0.$

De acuerdo con lo anterior, 4 puede escribirse como

\[ \pi(x ; q, r) = \big \vert C(x;q,r) \big \vert - \left \lfloor{\frac{1}{r}}\right \rfloor + \sum_{j = 1}^{\pi \left( \sqrt{x} \right) - d} (-1)^j \sum_{Q \in A_j(\sqrt{x} ; q)} \Big \vert C^*{\left( x; qQ, \left[ Q^{\varphi(q)} , qQ \right] \right)} \Big \vert, \] lo que finaliza la prueba.

Teorema 1 Sean $q,$ $r$ enteros no negativos tales que $r < q \leq x$ y $(q, r) = 1.$ Entonces \[ \sum_{j = 0}^{\pi\left( \sqrt{x}\right) - d } (-1)^j \sum_{Q \in A_j(\sqrt{x} ; q)} \left \lfloor{\frac{x - \left[ rQ^{\varphi(q)} , qQ \right]}{qQ}}\right \rfloor = \pi{\left(x; q, r \right)} - \pi \left( \sqrt{x}; q, r \right) + \left \lfloor{\frac{1}{r}}\right \rfloor, \tag{6}\] en donde $d = \big \vert D{\left(\sqrt{x} ; q \right)} \big \vert .$

Prueba. Para $Q \in A_j(\sqrt{x} ; q)$ con $j \geq 2$ se tiene que $\beta \left(\left[ rQ^{\varphi{(q)}} , qQ \right] \right) = 1,$ y por lo tanto \[ \sum_{j = 2}^{\pi{ \left( \sqrt{x} \right) } - d}(-1)^j \sum_{Q \in A_j(\sqrt{x} ; q)} \beta\left( \left[ rQ^{\varphi{(q)}} , qQ \right] \right) = \sum_{j = 2}^{\pi{ \left( \sqrt{x} \right) } - d}(-1)^j {\binom{\pi{ \left( \sqrt{x} \right) } - d}{j} } \tag{7}\] Por otro lado, como \[ 0 = (1 - 1)^{\pi{ \left( \sqrt{x} \right)} - d} = 1 - \pi{ \left( \sqrt{x} \right)} + d + \sum_{j = 2}^{\pi{\left( \sqrt{x}\right)} - d}(-1)^j \binom{\pi{\left( \sqrt{x}\right)} - d}{j}, \] entonces 7 puede escribirse de la forma

\[ \sum_{j = 2}^{\pi {\left( \sqrt{x} \right)} - d}(-1)^j \sum_{Q \in A_{j}{\left( \sqrt{x} ; q \right)}}\beta\left( \left[ rQ^{\varphi{(q)}} , qQ \right] \right) = -1 + \pi{\left( \sqrt{x} \right)} - d. \tag{8}\]

Note que para $Q \in A_{1}{\left(\sqrt{x} ; q \right)}$ se tiene que $\beta\left( \left[ rQ^{\varphi{(q)}} , qQ \right] \right) = 0,$ únicamente si $Q \in \{qk + r\}.$ De acuerdo con esto

\[ \sum_{Q \in A_{1}{\left( \sqrt{x}; q \right)}} \beta \left( \left[ rQ^{\varphi{(q)}} , qQ \right] \right) = \pi{\left( \sqrt{x} \right)} - \pi{\left( \sqrt{x}; q, r \right)} - d. \tag{9}\]

De las ecuaciones 8 y 9 se concluye que \[ \sum_{j = 1}^{\pi{\left( \sqrt{x} \right)} - d} (-1)^j \sum_{Q \in A_{j}{\left( \sqrt{x} ; q \right)}} \beta{\left( \left[ rQ^{\varphi{(p)}} , pQ \right] \right)} = \pi{\left( \sqrt{x}; q, r \right)} -1. \tag{10}\] Teniendo en cuenta 1, y al reemplazar 10en 2 obtenemos \[ \left \lfloor{\frac{x - r}{q}}\right \rfloor + \sum_{j = 1}^{\pi{\left( \sqrt{x} \right)} - d} (-1)^j \sum_{Q \in A_{j}{\left( \sqrt{x} ; q \right)}} \left \lfloor{\frac{x - \left[ rQ^{\varphi(q)} , qQ \right] }{qQ}}\right \rfloor = \pi{\left(x; q; r \right)} - \pi{\left( \sqrt{x} ; q , r \right)} + \left \lfloor{\frac{1}{r}}\right \rfloor. \] La prueba finaliza al iniciar la suma desde $j = 0.$

Residuos respecto a un entero común

Para un entero $x,$ escribiremos $N(x)$ para identificar el conjunto $N(x) = \{2, 3, \ldots , x\}.$ Note que $\big \vert N(x) \big \vert = x - 1.$

Se empleará la notación $C(x;q)$ para identificar el conjunto $\{ q k + \left[ x , q \right]\}_{k = 0},$ y con $B(x)$ identificaremos a la unión de estos conjuntos con $q \in P{\left( \sqrt{x} \right)},$ es decir \[ B(x) = \bigcup_{q \in P{\left(\sqrt{x} \right)}} C(x;q), \]

A partir de este momento asumiremos que $A_j(x) \equiv A_j(x; 1).$

Lema 2 Sean $p, q, x \in \mathbb{Z}$ con $p > 0.$ Entonces $p \vert (x - q)$ si y sólo si $\left[ q , p \right] = \left[ x , p \right].$

Prueba. Si $p \vert (x - q)$ entonces existe un entero $k$ tal que $x - q = pk.$ Por otro lado, existen enteros $k_1$ y $k_2$ tales que $\left[ x , p \right] = x - pk_1$ y $\left[ q , p \right] = q - p k_2,$ con lo que \[ \left[ x , p \right] -\left[ q , p \right] = p(k - k_1 + k_2). \] Como $0 \leq \left[ n , p \right] < p$ y $- p < - \left[ q , p \right] \leq 0,$ entonces \[ -1 < k - k_1 + k_2 < 1, \] y al ser $k,$ $k_1$ y $k_2$ enteros, la desigualdad estricta se cumple siempre que $ k - k_1 + k_2 = 0.$ Por lo tanto $\left[ q , p \right] = \left[ x , p \right].$

Si $\left[ q , p \right] = \left[ x , p \right]$ entonces, para enteros $k_1$ y $k_2$ como en la primera parte de la prueba, se verifica que \[ \begin{align*} x - pk_1 & = q - pk_2 \\ x - q &= p (k_1 - k_2), \end{align*} \] y en consecuencia $p \vert (x - q).$

Lema 3 $\big \vert N(x) \setminus B(x) \big \vert = \pi(x) - \pi(\sqrt{x}) + 1.$

Prueba. Se desprende del lema 2 que $q \notin B(x)$ si y sólo si $x - q$ es un número primo.

Por otro lado, note que para todo primo $p \leq \sqrt{x},$ se tiene que $x - p \in B(x),$

Lema 4 Sea $x$ un entero no negativo, entonces \[ \big \vert N(x) \setminus B(x ) \big \vert = \sum_{j = 0}^{\pi{\left( \sqrt{x} \right)}} (-1)^j \sum_{Q \in A_{j}(\sqrt{x})} \left( \left( \frac{x - \left[ x , Q \right]}{Q} \right) + 1 - d_{Q}(x)\right). \tag{11}\]

Prueba. Es claro que \[ \big \vert N(x) \setminus B(x) \big \vert = \Big\vert N(x) \setminus \bigcup_{Q \in P{\left( \sqrt{x} \right)}} C(x;Q) \Big\vert \]

De forma similar a la prueba del lema 1, note que si en el sistema 5 cambiamos $\left[ rQ_{i}^{\varphi(q)} , qQ_i \right]$ por $\left[ x , Q_i \right]$ para $i = 1, \ldots , n$ el sistema admite una solución elemental, siendo ésta $x.$ De acuerdo con lo anterior, para $Q \in A_j{\left( \sqrt{x} \right)}$ con $j \geq 2,$ se tiene que \[ \Big\vert C{\left(x; Q\right) }\Big\vert = \left( \frac{x - \left[ x , Q \right]}{Q}\right) + 1 - d_{Q}(x), \] lo que finaliza la prueba.

Lema 5 Si $x$ es un entero no negativo, entonces \[ \sum_{j = 0}^{\pi{\left( \sqrt{x} \right) } } (-1)^j \sum_{Q \in A_j(\sqrt{x})} \left( \frac{x - \left[ x , Q \right] }{Q} \right) = \pi{(x)} - \pi{\left( \sqrt{x}\right)} + 1. \tag{12}\]

Prueba. Note que \[ \sum_{j = 0}^{\pi{\left( \sqrt{x}\right)}} (-1)^j \sum_{Q \in A_j{\left( \sqrt{x} \right)}} 1 = \sum_{j = 0}^{\pi{\left( \sqrt{x}\right)}}(-1)^j \binom{\pi{\left( \sqrt{x}\right)}}{j} = 0, \]

de acuerdo con esto y el resultado del lema 3, la ecuación 11 puede escribirse en la forma \[ \sum_{j = 0}^{\pi{\left( \sqrt{x} \right)}} (-1)^j \sum_{Q \in A_{j}(\sqrt{x})} \left( \left \lfloor{\frac{x}{Q}}\right \rfloor - d_{Q}(x)\right) = \pi{(x)} - \pi{\left( \sqrt{x}\right)} + 2- \beta(x-1). \] Por otro lado, tenemos que \[ \sum_{j = 0}^{\pi{\left( \sqrt{x} \right)}} (-1)^j \sum_{Q \in A_{j}(\sqrt{x})} d_{Q}(x) = \sum_{j = 0}^{d} (-1)^j \sum_{Q \in A_{j}(\sqrt{x})} 1 = 0, \] en donde $d = \vert D (\sqrt{x} ; x)\vert,$ lo que finaliza la prueba.

Es conocido que \[ \sum_{j = 0}^{\pi(\sqrt{x})}(-1)^j\sum_{Q \in A_j(\sqrt{x})} \frac{1}{Q} = \prod_{p \leq \sqrt{n}} \left( 1 - \frac{1}{p}\right), \] y si escribimos \[ R(x) = \sum_{j = 0}^{\pi{\left( \sqrt{x} \right) } } (-1)^{j+1} \sum_{Q \in A_j(\sqrt{x})} \left\{ \frac{x}{Q} \right\} , \tag{13}\]

entonces, una consecuencia inmediata del teorema anterior es

Corolario 1 Para todo entero $n \geq 2$ se verifica

\[ \label{eq::final0} n \prod_{p \leq \sqrt{n}} \left( 1 - \frac{1}{p}\right) - R(n) = \pi{(n)} - \pi{\left( \sqrt{n}\right)} + 1. \tag{14}\]

Para algunos casos elementales, la ecuación $\eqref{eq::final0}$ permite encontrar el número de primos hasta un cierto $n,$ cuando se conoce de manera exacta el valor de $R(n),$ o un valor aproximado del mismo. Puede comprobarse esto tomando $n = 6, 12, 18, 24, 30,$ valores de $n$ para los cuales $R(n) = 0,$ y $\phi(\sqrt{n})$ es fácilmente computable.

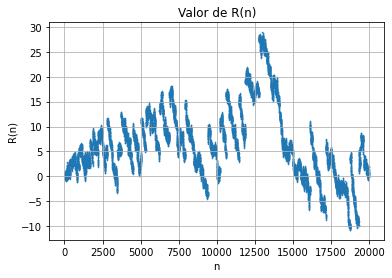
la siguiente figura es una representación del gráfico $R(n)$, con $n$ desde 2 hasta 20000.